Array multidimensi dengan dua dimensi sering digunakan untuk merepresentasikan tabel nilai-nilai yang terdiri dari informasi yang diatur dalam baris dan kolom. Untuk mengidentifikasi elemen tabel tertentu, kita harus menentukan dua indeks. Dengan konvensi, yang pertama mengidentifikasi baris elemen dan kolom kedua. Array yang membutuhkan dua indeks untuk mengidentifikasi elemen tertentu disebut array dua dimensi. (Array multidimensi dapat memiliki lebih dari dua dimensi.) Java tidak mendukung array multidimensi secara langsung, tapi itu tidak memungkinkan programmer untuk menentukan array satu dimensi yang elemen-elemennya juga array satu dimensi, sehingga mencapai efek yang sama.
Gambar diatas menggambarkan array dua dimensi yang berisi tiga baris dan empat kolom (yaitu, tiga-by-empat array). Secara umum, sebuah array dengan m baris dan n kolom disebut array m-oleh-n.
Contoh : int b[][] = { { 1, 2 }, { 3, 4 } };
Contoh membuat array 2 dimensi :
int b[][];
b = new int [ 3 ][ 4 ];
Lalu bagaimana implementasinya : array 2 dimensi sering digunakan membuat tabel dan matriks dalam matematika, untuk membuat tabel sudah dijelaskan melalui gambar diatas, sedangkan matriks belum dijelaskan. Dalam, Matematika, matriks adalah kumpulan Bilangan, simbol, atau Ekspresi, berbentuk Persegi Panjang Yang disusun * Menurut Baris Dan kolom. Bilangan-Bilangan Yang terdapat di suatu matriks disebut Artikel Baru elemen atau anggota matriks. Contoh matriks Artikel Baru 2 Baris dan 3 kolom yaitu :
Disini Saya Akan menunjukkan Cara Kerja Array 2 pada dimensi Dalam, perhitungan matriks, Yang terdiri Bahasa Dari penjumlahan matriks, perkalian matriks Dan transpos dengan menggunakan bahasa pemrograman java
/ / Menambahkan nilai suatu Matrik dengan Matrik Lain
publik Matrik tambah (Matrik b) {
Matrik a = this;
Matrik c = new Matrik (nBaris, nKolom);
if (a.nBaris == b.nBaris && a.nKolom == b.nKolom) {
for (int i = 0; i <nBaris; i)
for (int j = 0; j <nKolom; j)
c.itemDt [i][j] = a.itemDt [i][j] b.itemDt [i][j];
}
return c;
}
/ *
* Perkalian antara dua vektor yang berbeda
* /
public Matrik_kali (Matrik b) {
Matrik a = this;
Matrik c = new Matrik (a.nBaris, b.nKolom);
if (a.nBaris == b.nKolom)
for (int i = 0; i <c.nBaris; i)
for (int j = 0; j <c.nKolom; j)
for (int k = 0; k <a.nBaris; k)
c.itemDt [i][j] = (a.itemDt [i][k] * b.itemDt [k][j]);
return c;
}
/ *
* Membuat transposisi dari suatu Matrik
* /
publik Matrik transposMatrik () {
Matrik a = new Matrik (nBaris, nKolom);
for (int i = 0; i <nBaris; i)
for (int j = 0; j <nKolom; j)
a.itemDt [j][i] = this.itemDt [i][j];
return a;
}
Sumber
Author: dinda-dinho
Related Posts
Some simillar article from this label, you might also like
Keyword Super()Pengertian Keyword Super Keyword super biasa digunakan dalam OOP (Objek Oriented Programing) terut
Inheritance dan Contohnya Pengertian Inheritance (Pewarisan) Inheritance (penurunan sifat / pewarisan), ini merupakan ciri
Source Code Inisialisasi USB Source Code Inisialisasi USB - Setelah mengetahui bagaimana proses inisialisasi dari USB yang a
Download Ebook Algoritma dan Struktur dataDownload Ebook Algoritma dan Struktur Data : Bab 1 : Arrays Bab 2 : Simple Sorting Bab 3 : Stack an
Proses Inisialisasi USB Proses Inisialisasi USB - Sebelum membahas bagaimana proses inisialisasi USB, alangkah baiknya jik
Sorting dengan Metode Selection Sort Ini adalah post lanjutan dari post Metode Bubble Sort. Kali ini akan dijel
Previous Post
Pengertian dan Konsep Binary Tree
Pengertian dan Konsep Binary Tree
Subscribe to:
Post Comments (Atom)


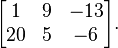
pranala lain -> MENGENAL ARRAY BERDIMENSI BANYAK
Reply